Mathematical interpretation of DCM
Since the way a frame can be built from the structure of other frames is the most fundamental operation in DCM, it makes sense to give it some formal grounding.
There are two constructs in mathematics that correspond to this operation: fibre bundles (topology) and wreath products (group theory). We will use EXCHANGE frame as an example.
Fibre Bundle interpretation
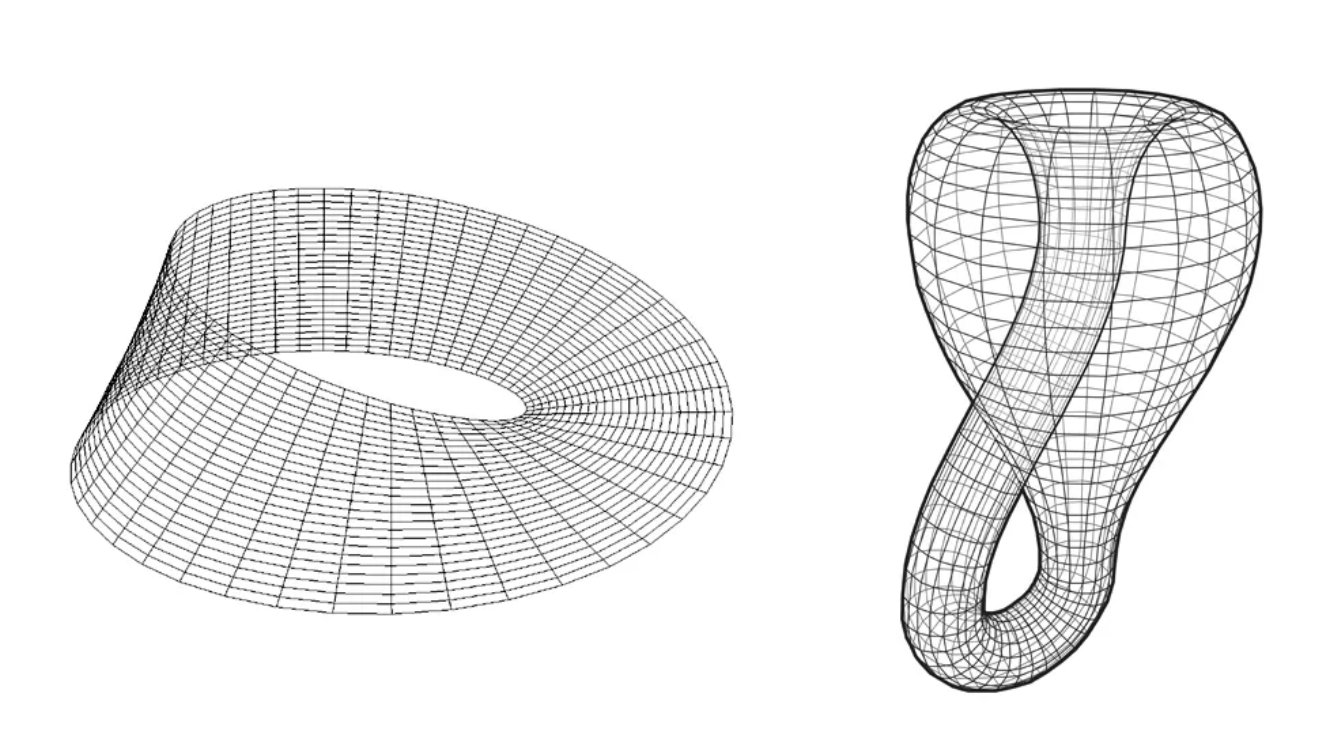
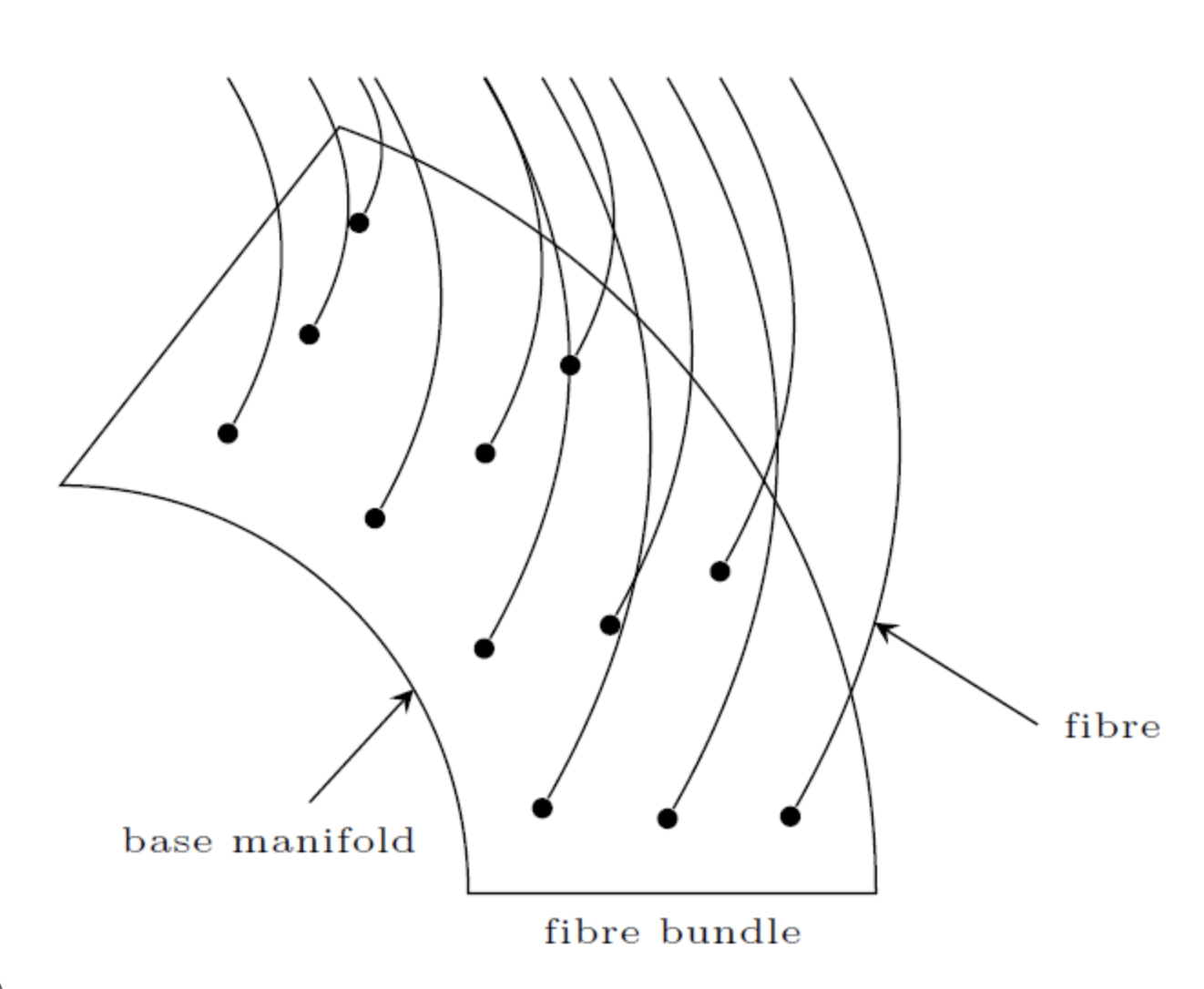
The structure of the EXCHANGE frame in isolation (without its two components) serves as the base space, while each MOV_SYNC instance functions as a fibre. Note that, due to this correspondence, these component frame instances are referred to as fibres in DCM.
The structure of the EXCHANGE frame together with its components (i.e. the whole EXCHANGE construal) forms the total space. The bindings for each MOV_SYNC component act as projection maps.
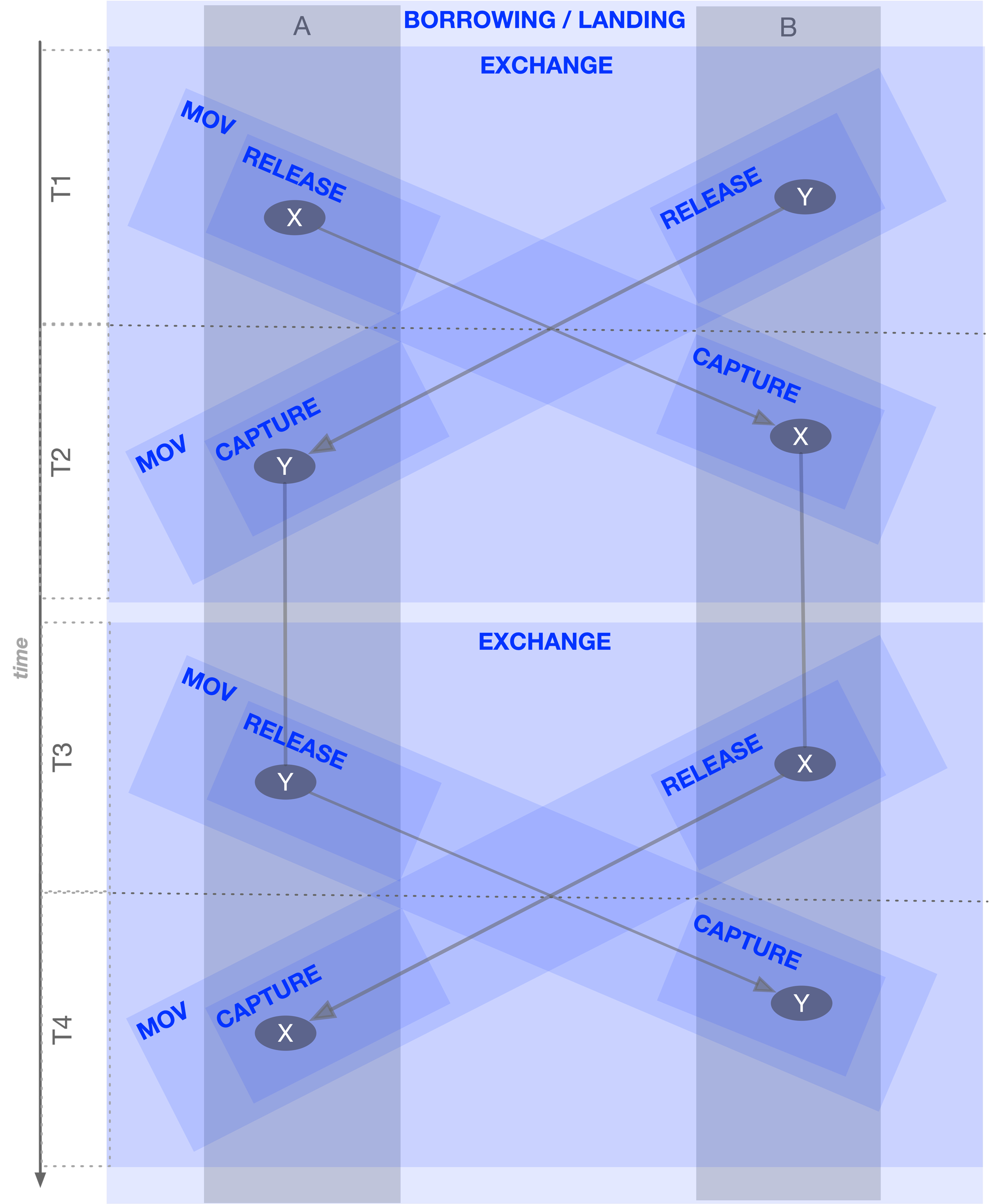
If we take the EXCHANGE frame as a base space and RELEASE as a fibre, the resulting total space would consist of two RELEASE frames—one releasing A, and the other releasing B.
As will be shown elsewhere, a more complex frame like BNL (Borrowing and Lending) involves two EXCHANGE fibres as the opening and closing legs, along with an additional MOV_SYNC fibre representing a fee. Thus, for the BNL base space, there will be:
2 fibres of EXCHANGE
5 fibres of MOV_SYNC
5 fibres of RELEASE
5 fibres of CAPTURE
And this is even before contextualizing the contract with other contracts. As we will see, executing a TRADE frame requires contextualization with many other frames to make settlement executable. In this contextualized version of a TRADE, there will be 22 RELEASE fibres, while a BNL frame will have 55.
This illustrates the potential mathematization of the trading domain — transforming it from an informal system of conventional and dispositional encodings into a formal system with rich inferential (entailment) structure and thus with rich semantics.
Wreath product interpretation
Another existing mathematical construction that models this situation is the wreath product from group theory in abstract algebra.
A wreath product is formed by the action of one group on many copies of another group — the former group creates the copies and adjusts or aligns each one differently.
It is essentially a mathematical model of cut-and-paste.
In this analogy, the EXCHANGE frame serves as the acting (or control, or top) group, while MOV_SYNC is the base (or bottom) group.
The construal in DCM (any non-trivial one like TRADE) is thus an iterative wreath product as it is a result of repeatedly applying the wreath product construction.
Natural Transformation
DCM itself is intended to create a model of the relevant part of the business domain, and thus to stand in a modelling relation to it.
The mathematical interpretation of the modelling relation is given by the notion of a natural transformation in category theory (see the Modelling Relation section for more details).